An old story tells of a Maths professor, who at a certain point in his lecture told the class, "The proof of this is obvious", but then began to have doubts. After gazing at the blackboard for some time he said, "Hmmm. Perhaps it's not obvious. I'll have think about it and let you know in next week's lecture."
The following week the class assembled, and after a new minutes the professor arrived. Gazing round the lecture theatre, he said "Since our last lecture I have been thinking about that problem in every waking hour, but I simply could not see it. But you will be glad to know that on my way here today I finally saw the answer."
"It
is obvious."
Well, I have been thinking for several days about how to prove the Conway Circle Theorem, a rather nice result usually credited to the brilliant and original mathematician John Horton Conway, who sadly died in the recent Covid Pandemic. I could fairly quickly see a proof but it had a rather messy feel to it, it wasn't anything I would want to explain on this blog. It wasn't what I would call elegant. I felt there must be a nicer proof, one that would make the proof of the theorem, well, obvious.
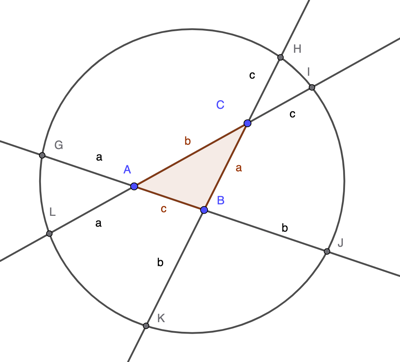
After much chewing the problem over I think I have a proof which does make the theorem fairly obvious. But I'd better tell you what the theorem is before we go any further. Consider the following diagram.
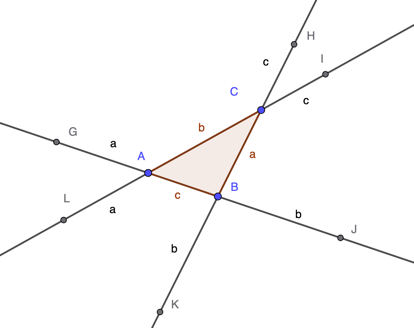
As shown in the diagram, the three sides of triangle ABC have each been extended at both ends, AB by distances a and b, BC by distances b and c, and CA by distance c and a. This gives the six points G, H, I, J, K, L. Conway's theorem says that (rather surprisingly) these six points lie on a circle, see below:
How to prove this? I'm going to use some well-known properties of isosceles triangles, triangles with two sides equal in length.
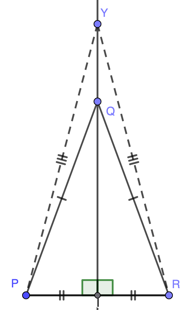
In triangle PQR sides PQ and QR are equal. The line bisecting the base PR at right angles, the
perpendicular bisector, must pass through the apex Q, and it bisects the angle PQR. Moreover any point, for example Y, that lies on the perpendicular bisector is equidistant from points P and Q, as shown by the dotted lines.
Going back to our original diagram, let's join up the six points to make a hexagon, and then draw in the perpendicular bisectors of its sides, shown dotted:
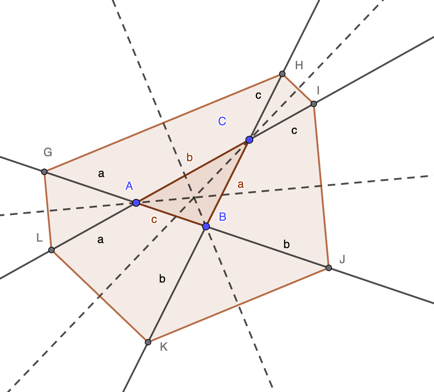
We see that each side of the hexagon is the base of a triangle, which by the method use to construct the six points must be isosceles. Each perpendicular bisector passes through a vertex of triangle ABC and bisects the angle there, and is fact the shared perpendicular bisector of a pair of the hexagon's sides lying opposite one another.
It's well known that the three lines bisecting the angles of a triangle meet in a single point, called the
incentre. Because the three dotted lines bisect the angles of ABC this mean they meet at its incentre.
Because the incentre is on the perpendicular bisector of HI it must be equidistant from H and I. Similarly because it is on the perpendicular bisector of IJ it must be equidistant from I and J. By the same argument, it must be equidistant from J and K; from K and L; from L and G; and from G and H. Thus it is equidistant from all six points and is the centre of a circle that passes through them all.
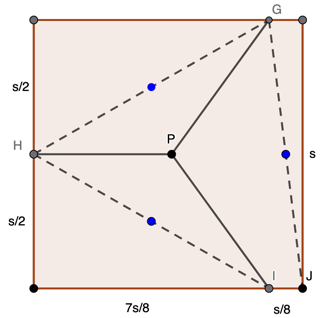
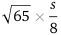 . The ranger stations are at the midpoints of the diameters (blue dots) and the further distance of travel ever needed is
. The ranger stations are at the midpoints of the diameters (blue dots) and the further distance of travel ever needed is 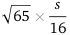 ≈ 0.504s.
≈ 0.504s.