The round tuit (that you haven't got one of).
The jump tuit and the hop tuit.
The up tuit (that you don't fee0.
The round tuit (that you haven't got one of).
The jump tuit and the hop tuit.
The up tuit (that you don't fee0.
I thought I was buying jellied eels but it turned out to be a special offers on selected jellies.

At last! After decades of toil in my Alchemical Laboratory, I have found the Elixir of Life.
Turns out to be a thin watery soup, which I’ve named The Holy Gruel.
ChatGTP, an online AI engine, came up with this, which is not bad
Why did the cat join the Red Cross? Because she wanted to be a first-aid kit!

Cirse
Peru
Plume
Winberge
Æppel
Blækberie
EhoÞberge
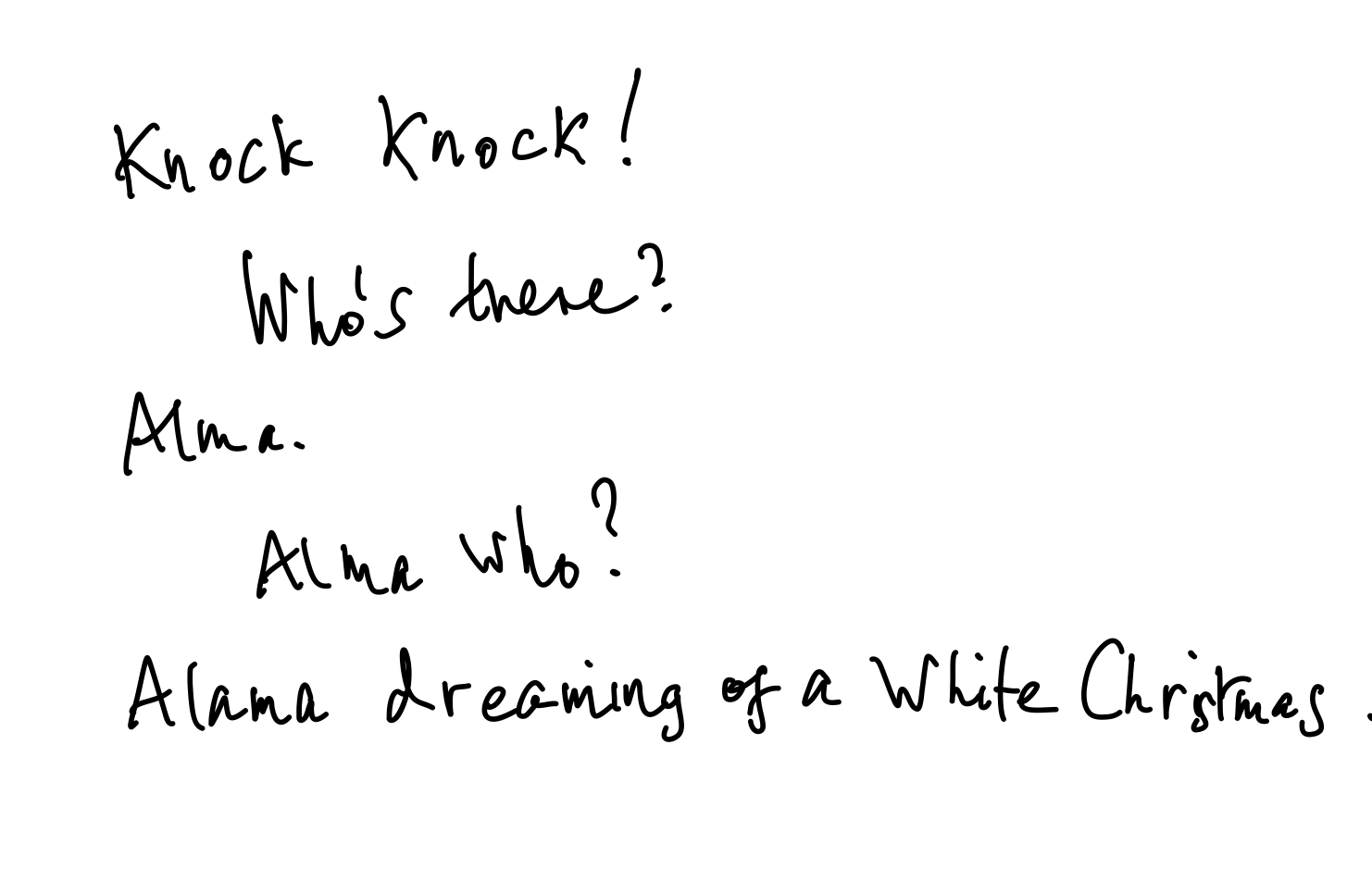
Who’s there?
Lenny.
Lenny who?
Lenny snow, Lenny snow, Lenny snow!
Smoked Salmon with Tarragon and Lemon Juice dressing.
Sorry, 2 got clipped
What interesting facts do you notice about how the corners of this cube are numbered?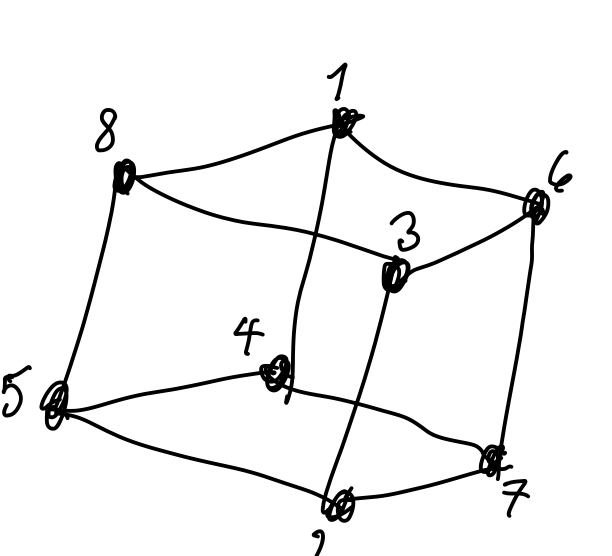
I've just watched this marvellous lecture, given tonight at the Royal Institution. The speaker was Andrew Szydlo, who is an engaging mix of educator, scholar of the history of science, subject enthusiast, and showman.
The beautiful image above (flames not ghosts!) is one of the many demonstrations in the lecture. This one illustrates how compounds of different chemical elements produce characteristic colours in flames. The lecture made the point, which I'd never thought about before, that this must have been observed for possibly thousands of years, although the substances behind these colours were not understood in terms of elements in the modern sense. That idea has only been around for a couple of hundred years.
To give you an idea of the lecture's scope, it covered, amongst other things: the discovery and recognition of hydrogen as a gas, distinct from air; its connection with water, which gives it its name "Water producer"; ways of producing hydrogen; its use in ballooning and how then R101 disaster destroyed that dream; its use in rocketry that sends satellites up into orbit; its explosive properties when mix with oxygen; the discovery of gaseous diffusion; the role of hydrogen in the revelling of spectral lines; its seminal role in the beginning of quantum physics is; pH and acidity of fruits; and the fact that 78% of the universe is Hydrogen, first discovered by the brilliant Cecilia Payne-Gaposchkin.
To find the YouTube video, just Google The Explosive History of Hydrogen Royal Institution.
I asked an AI Bot to write me a sonnet on cheese in the style of William Shakespeare and this is what I got.
Oh, cheese of creamy goodness, fair and fine Thou art the source of endless gustatory delight Thy savory flavor, a symphony divine Makes every taste bud dance with pure joy and excite
In thy texture, oh cheese, so rich and smooth Thou art the queen of all culinary arts Thy melted form, a culinary treasure to behold Thou bringest joy to the heart of cheese lovers and food connoisseurs alike
Thy variety, oh cheese, is truly staggering From cheddar to gorgonzola, brie to feta Thou art the star of many a fine dining And the perfect companion to a crisp glass of wine
Oh cheese, thou art the soul of many a dish
Thy flavour and texture, a culinary bliss.
F. D. C. Williard was a cat whose scientific papers were published internationally.
Williard was a Siamese owned by Jack H. Hetherington. Hetherington wanted to publish some of his work, but discovered that his journal of choice had a policy that papers with single authors must write in the first person singular, "i" , and not research to the author as "we".
This was in 1975 and the task of retyping the manuscripts would have been formidable at that time.So Hetherington decided to add his cat Chester as co-author, under the nom de plume F. D. C. Williard. The paper was published and F. D. C. Williard became quite celebrated, publishing a paper as sole author, and often being mentioned by other scientists in footnote, where they thanked please invaluable contributions to the discussion etc etc.
You can read all about this notable cat here.

A ruthless rhyme by Harry Graham
Little Willie, full of glee,
Put radium in grandma’s tea.
Now he thinks it quite a lark
To see her shining in the dark.
More to follow
This is something I read a long time ago, I can’t remember where. Someone spotted a sign that read
and wondered did it mean
1. Alsatians roaming freely.
2. Sexually incontinent outstations.
3. Alsatians with poor bowel control.
4. A demand that Alsatians be released from captivity.
5. Alsatians for sale in arbitrary numbers, not pre-bagged.
And I suppose we might add
6. Floppy Alsatians.
Interviewer: Adventurous Chicken, why did you cross the road?
Adventurous Chicken: Because it was there. Plus, someone had to do it.
“That’s a whole Pandora’s box of worms you’ve opened up.”
This blog might contain posts that are only visible to logged-in users, or where only logged-in users can comment. If you have an account on the system, please log in for full access.